|
Hi, I'm Aayush! I'm currently a PhD student in Computer Science at Harvard, advised by Prof. Sitan Chen and Prof. Yilun Du. Broadly, I am interested in developing algorithmic techniques that enhance the capabilities of modern generative models. My research seeks principled algorithms that are empirically performant, often leveraging theoretical arguments in well-designed toy settings, to advance fundamentally intelligent behaviors such as reasoning, reward-optimization, and self-correction/failure prediction. I graduated from Harvard in 2023 with an AB/SM in Physics, Mathematics, and Computer Science. As an undergrad, I explored research in a variety of fields across pure mathematics, computational biology, and theoretical physics. |

|
||||||||||||||
Recent News
|
|||||||||||||||
|
|
|
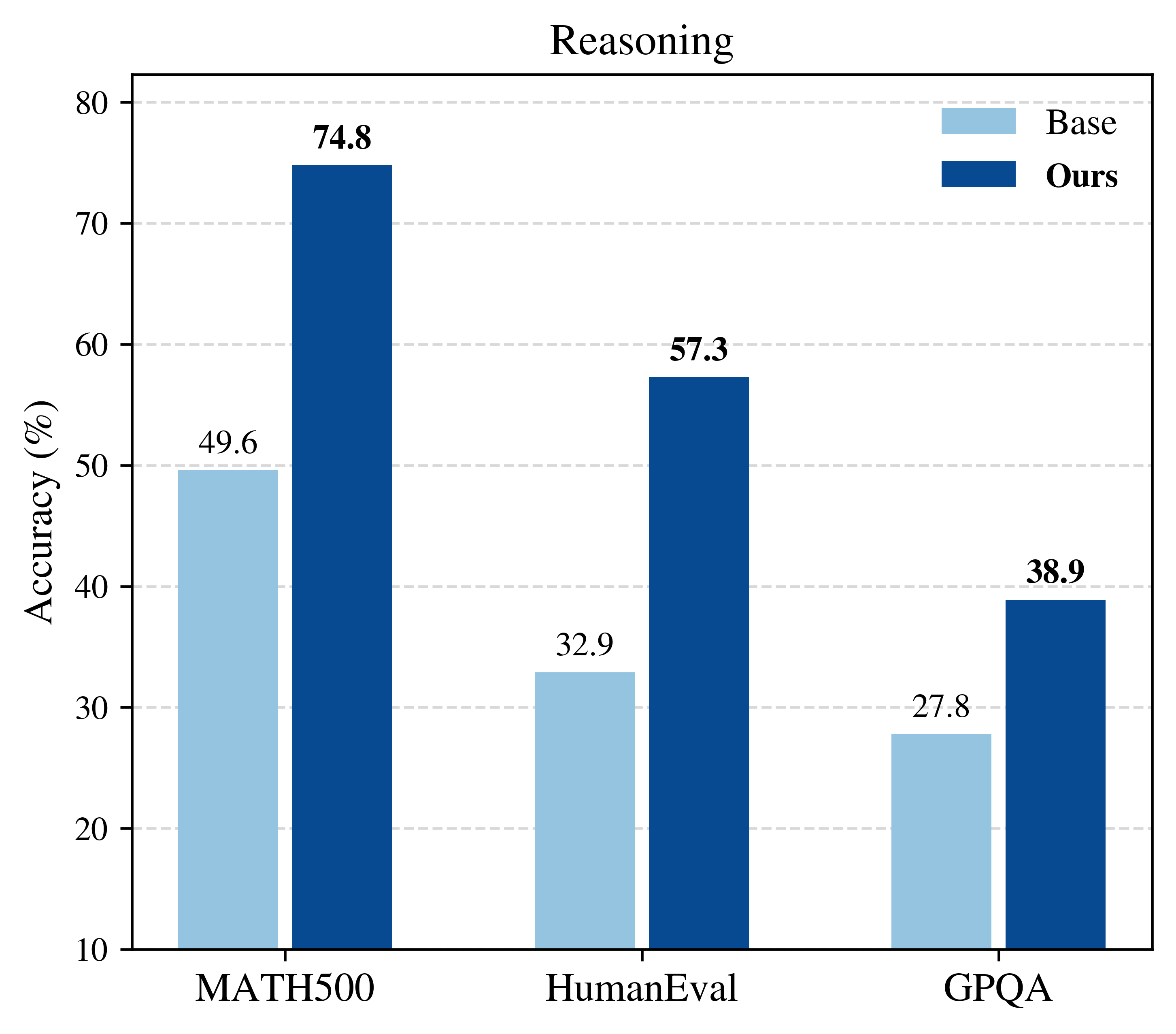
Aayush Karan, Yilun Du arXiv preprint, 2025 blog post / paper / code / tweet We propose a sampling algorithm for base models that gives single-shot reasoning boosts on par with RL-posttraining, without compromising generation diversity and multi-shot (pass@k) performance. Crucially, our method is training-free, dataset-free, and verifier-free. |
|
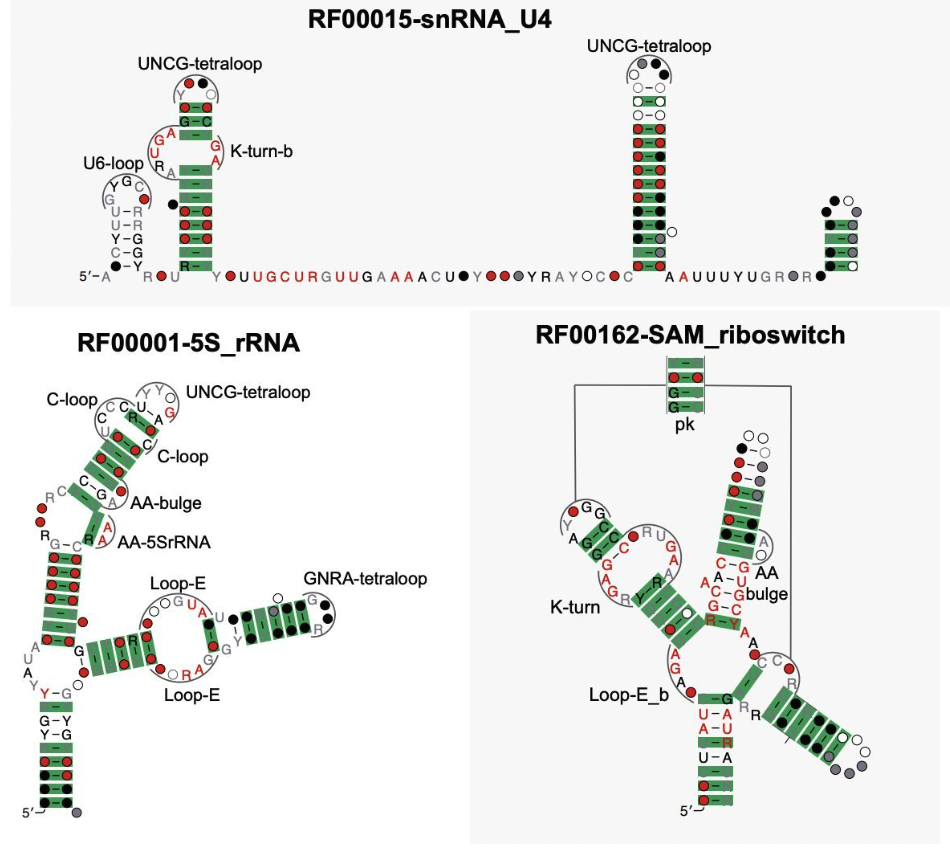
Aayush Karan, Elena Rivas Nature Methods, 2025 paper / code / tweet The field of RNA structure prediction has long lacked a reliable, flexible, and self-contained method to detect the presence of key 3D building blocks in folded RNAs. We provide an algorithm that does exactly this, predicting a near exhaustive set of 3D configurations (everything), at any location (everywhere), fully end-to-end over multiple structural hierarchies (all-at-once). |
 
|
Aayush Karan, Kulin Shah, Sitan Chen arXiv preprint, 2025 paper / tweet We discover that strong latent initializations in noise space offer a new axis for desiging inference-time algorithms that steer diffusion models towards reward functions. We propose a simple algorithm (ReGuidance) leveraging this insight and both empirically and theoretically demonstrate its superiority over prior techniques. |
|
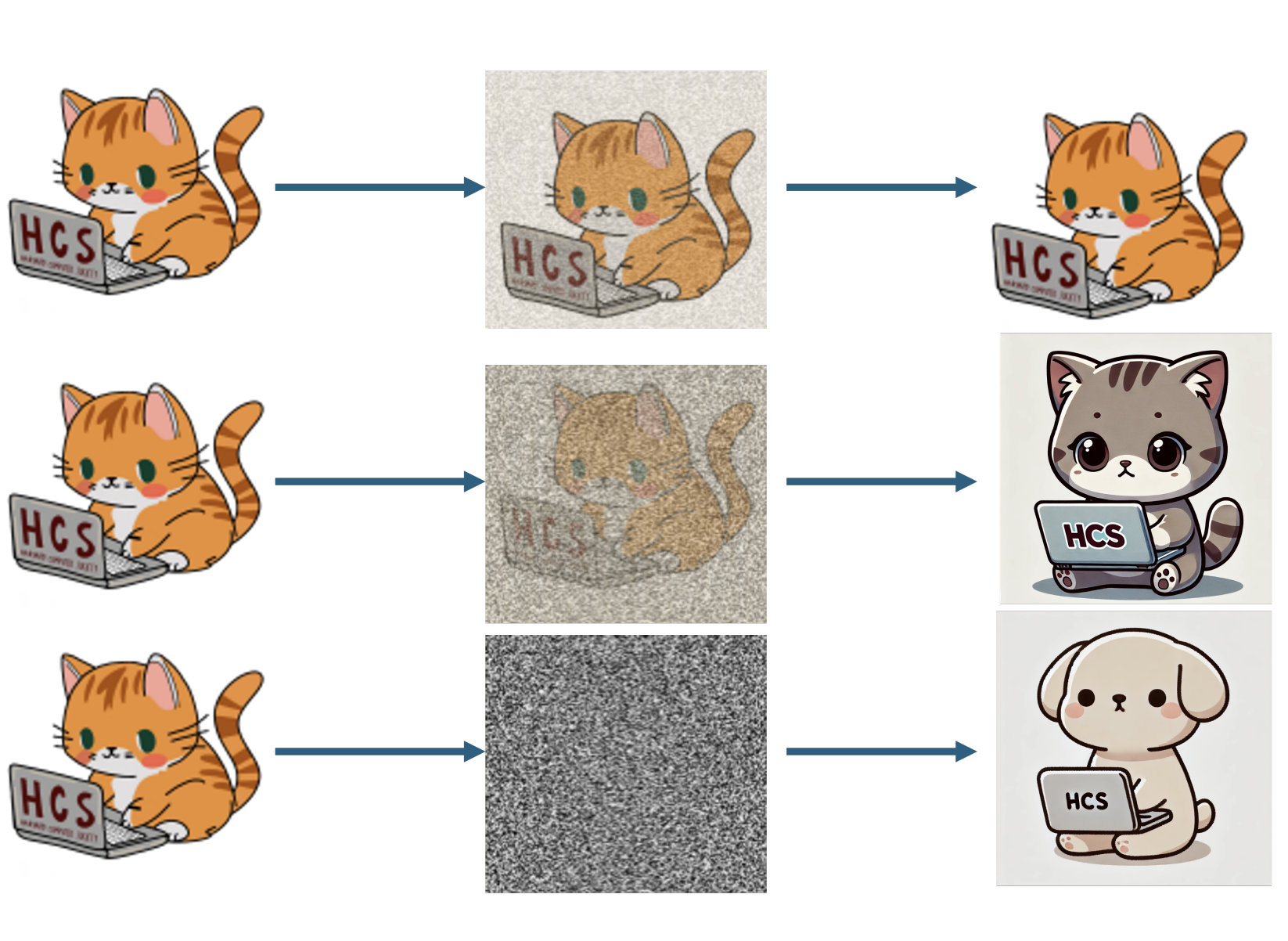
Marvin Li, Aayush Karan, Sitan Chen ICML, 2025 (Oral, top 1% of submissions) paper / tweet We present a unifying theory of LLMs and diffusion models explaining the sudden emergence of high-level semantic features during generation. We introduce the notion of critical windows for LLMs and empirically correlate them to reasoning failures. |
|
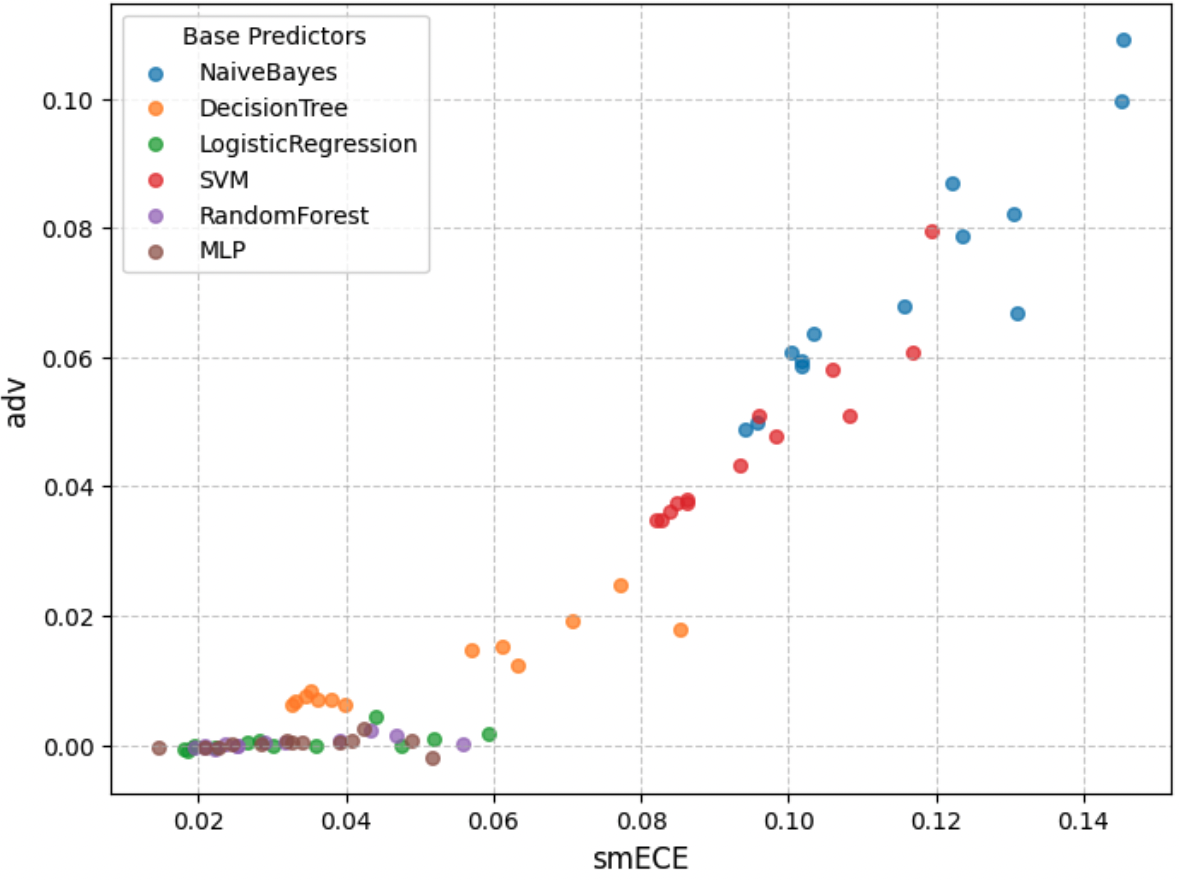
Aravind Gollakota, Parikshit Gopalan, Aayush Karan, Charlotte Peale, Udi Wieder FORC, 2025 paper / tweet We present a theory of loss prediction in machine learning and establish an equivalence with algorithmic fairness. In particular, we prove that for binary classifiers, we can learn a nontrivial loss predictor only when the base model is not multicallibrated. |
|
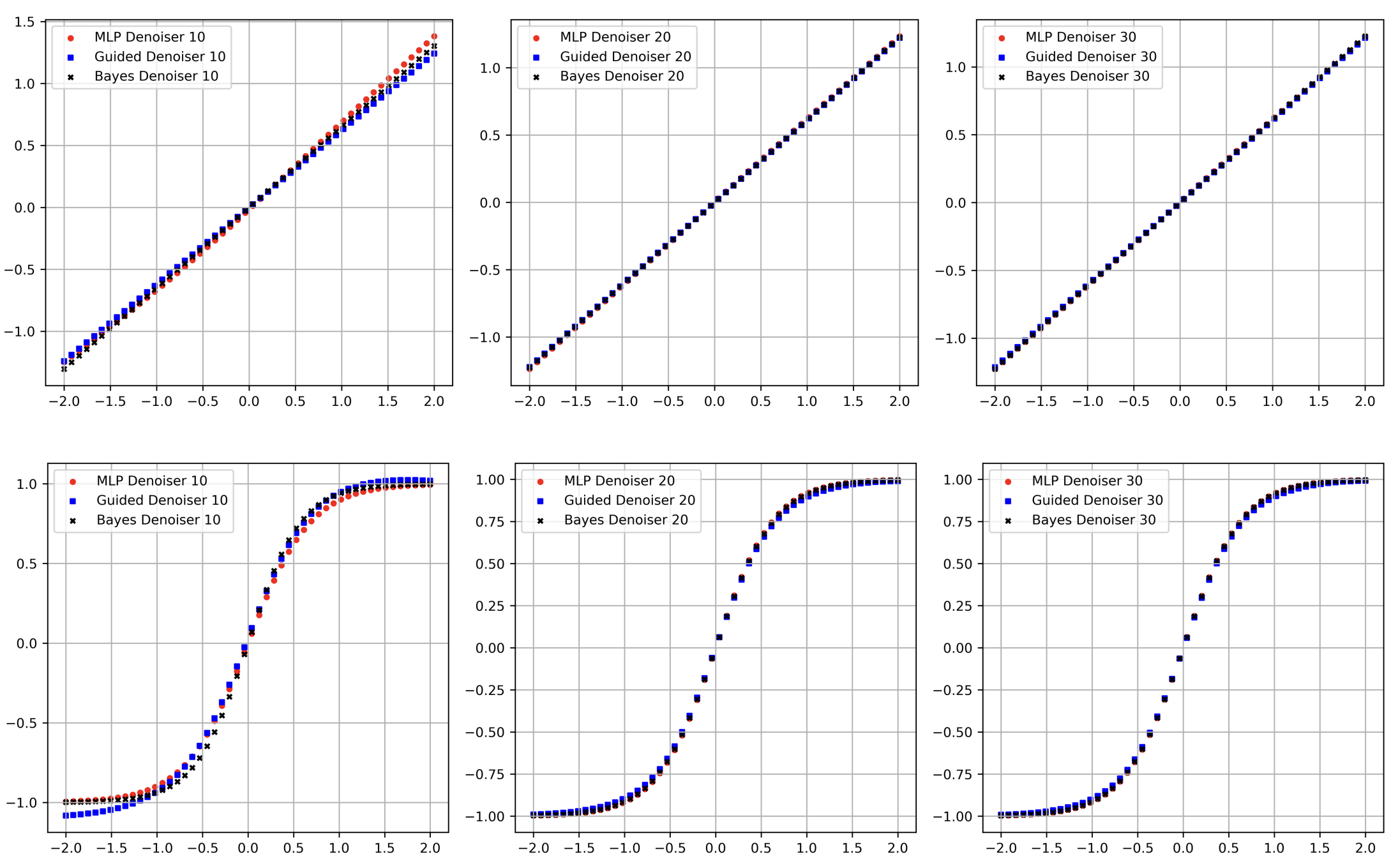
Aayush Karan, Kulin Shah, Sitan Chen Yonina Eldar NeurIPS, 2024 paper / tweet We propose a theory-inspired neural network architecture for solving inverse problems that provably learns optimal Bayesian inference. Our network mirrors diffusion models by learning noisy data priors and runs a Bayes-optimal algorithm on top. For the first time in the literature, we prove that the score-matching objective is learnable in one dimension. |
|
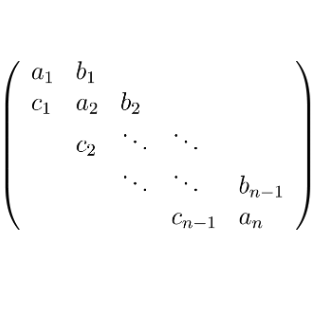
Aayush Karan Journal of Algebra, 2022 paper We examine a pair of linear maps with a particular property (tridiagonal pairs) inspired from statistical physics, and we demonstrate that linear perturbations preserve this property under a very simple polynomial condition. |
|
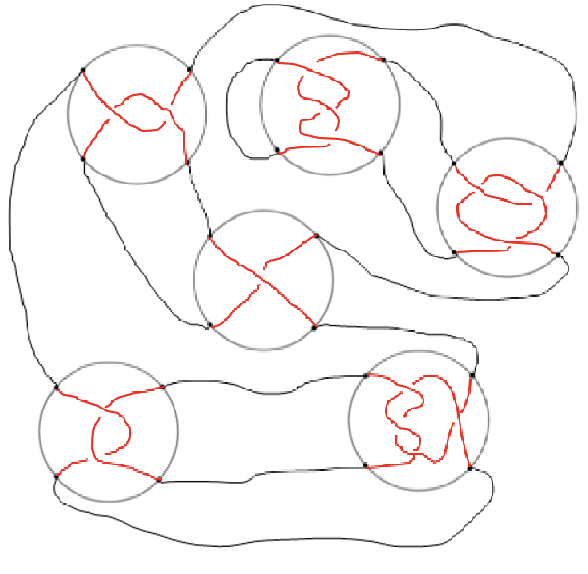
Aayush Karan Topology and its Applications, 2019 paper We resolve an open problem proposed by David Mullins in 1993 regarding the recursive computability of crucial topological quantities known as nonzero determinant link invariants. |